Dal libro di Giuseppe Aragosa “Da Saticula alle Terre dei Gambacorta” una ricostruzione della groma, antico strumento per tracciare allineamenti e misurare le distanze
L’ultimo libro di Giuseppe Aragosa, “ Da Saticula alle Terre dei Gambacorta” è un saggio di respiro vasto, che mentre affronta in maniera scientifica, basandosi su un’attenta lettura delle fonti storico-letterarie e delle indagini archeologiche, lo studio sull’ubicazione dell’antica città sannita di Saticula, poi distrutta dai Romani, allo stesso tempo consente al lettore di apprezzare particolari e curiosità sugli usi, i costumi, le caratteristiche del lavoro, e la gestione del Territorio da parte delle antiche popolazioni della Campania Greco-Romana.
In questo senso, la Centuriazione Romana, ossia la razionale suddivisione del territorio in centurie, appezzamenti quadrati di 200 iugeri, articolati perpendicolarmente alle due linee di distribuzione spaziale fondamentale, tra loro perpendicolari, il Cardo e il Decumano, diventa l’occasione per parlare dello strumento con i quale i Romani tracciavano i loro allineamenti, e i solchi fondamentali dei Castra.
Questo strumento e la Groma.
Nel libro si trova una schematizzazione del funzionamento della Groma e la sua ricostruzione grafica.
dal libro “Da Saticula alle Terre dei Gambacorta”
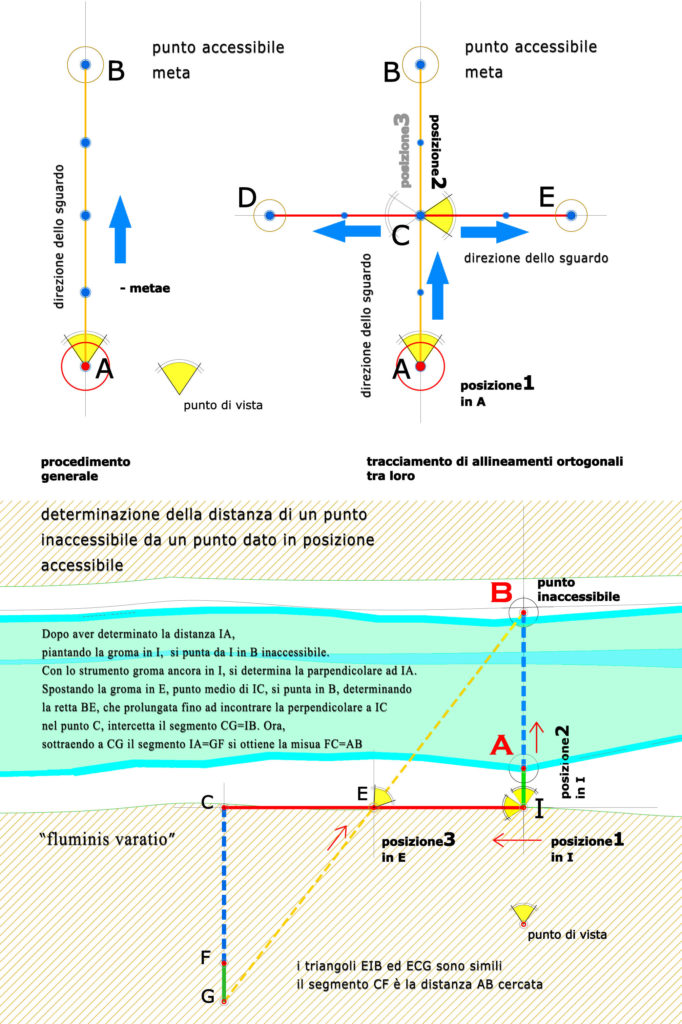

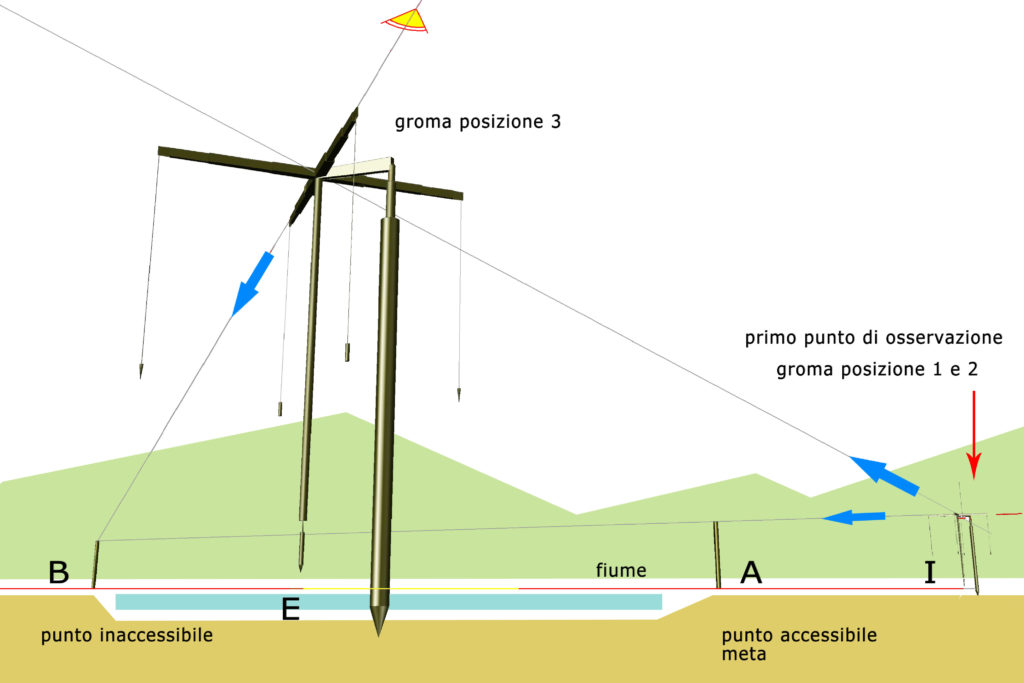
fig .1 determinazione di un punto inaccessibile
fig. 2 determinazione di un punto inaccessibile

fig. 3 la groma, ricostruzione



1 commento
Marco De Donno · 09/12/2019 alle 7:37
Molto bella la grafica qui riproposta come “figura 1” per la spiegazione del metodo di determinazione di un punto inaccessibile disponendo solo di uno strumento in grado di traguardare squadri e –debbo immaginare- di uno strumento di misurazione lineare.
Così chiara che per la prima volta mi si aprono interrogativi ai quali non avevo mai pensato: lasciando perdere il fiume e ragionando di un campo completamente libero, forse -operando in questo modo sul presupposto geometrico delle proprietà dei triangoli- tracciamento e misurazione potrebbero risultare alla fine attendibili (solo con un margine di imprevedibilità dell’orientamento complessivo) anche nel caso in cui lo strumento utilizzato fosse leggermente starato (cioè con bracci costruttivamente non perfettamente ortogonali), alla sola condizione di ripetere l’identico errore nelle differenti stazioni?
Allora forse completando l’operazione con la costruzione di altri due punti (attorno ad E sul prolungamento dei segmenti GC e di BA) ed avendo cura di utilizzare sempre l’angolo sotteso fra i medesimi due bracci dello strumento (per ripetere un identico errore ove ve ne fosse) si potrebbe arrivare a costruire un quadrangolo corretto anche avendo a disposizione uno strumento di misurazione angolare inizialmente inaffidabile?
Se così fosse, facendo alla fine stazione in posizione centrale (in E) si disporrebbe di una serie di punti materializzati sul campo sulla base dei quali verificare ed eventualmente tarare correttamente lo strumento per gli utilizzi successivi.
Solo una idea, bisognerebbe ragionarci meglio.